Aritmética sencilla y el pensamiento lateral

No se trata de un problema de ‘pensamiento lateral’ en sentido estricto, aunque por su enunciado… lo parece. Lo planteó un usuario en Twitter y dice así:

“Tal y como muestra la imagen, se plantea el siguiente ejercicio:
Calcular 230-220*0,5.

Al tiempo se indica que su resultado es… 5!
Una respuesta con la que muchos no se mostraron de acuerdo.

En apariencia, el problema es muy sencillo, pues para su resolución solo hay que realizar dos operaciones simples de aritmética: una multiplicación y una resta.

¿Es correcta la respuesta? Si no fuese así: ¿Cuál sería?”

En el tuit de KJ Cheetman también se puede leer lo siguiente:

«Un meme matemático que es más divertido que estúpido”.
“Aunque no lo creas, la respuesta es 5!”

La solución en un próximo post.

============================================================================

A continuación mostramos la solución al problema planteado en el post: «Divisibilidad del número 37, truco o realidad matemática».

Se trata de una realidad matemática válida para cualquier número de tres cifras iguales.

Supongamos un número genérico de tres cifras: AAA.
Su valor, teniendo en cuenta las unidades, decenas y centenas, sería:
A+ A*10+ A*100
Siguiendo lo indicado en el enunciado del problema resultaría:
A+ A*10+ A*100/ A+A+A= A (1+10+100)/ 3A
Es decir:
111/3= 37

Por tanto cualquier número de 3 cifras iguales es divisible por 37.

Divisibilidad del número 37, truco o realidad matemática

Las Matemáticas a veces son complicadas, aunque no siempre tanto como parecen. Si se intenta resolver un problema, y no se encuentra el camino adecuado, antes de darse por vencido es necesario probar a cambiar su enfoque. Por su carácter técnico tienen vertientes diversas. Por sencilla que esta sea, en ocasiones cualquier excusa es válida para no insistir en la búsqueda. Este es el caso que nos ocupa, pues más que un problema es casi una diversión. Dice así:

“La regla de la divisibilidad del número 37 ofrece un efecto curioso. Establece que cualquier número de 3 cifras iguales es divisible por 37 como se puede comprobar en la figura adjunta.¿Tiene truco? ¿Es una realidad matemática? ¿Por qué?

Ver solución en «Aritmética sencilla y el pensamiento lateral».

=====================================================================

A continuación mostramos la solución al problema planteado en el post: «Las hijas del rajá, las perlas y un reparto equitativo».

La propuesta del rajá parece algo complicada, pero es correcta. Además, según el dictamen del juez no perjudica a ninguna de sus hijas: todas reciben el mismo número de perlas. Veamos como llegar a esta conclusión mediante una ecuación algebraica.

Llamando x al número total de perlas, según se indica en el enunciado del problema se puede establecer la siguiente ecuación entre las perlas recibidas por las dos primeras hijas.

Que una vez desarrollada nos lleva a:

El número total de perlas a repartir es 36.

Conociendo este dato, ya se puede calcular el número de hijas.
Así, por ejemplo, la primera (y todas las demás) recibiría: 1+1/7 (36-1)=6 perlas. Como el total de perlas es 36  y lo que recibe cada una son 6, el número de hijas es 6 (36/6).

Con los datos obtenidos, y como comprobación final, veamos como el reparto entre las 6 hijas es equitativo y cumple con lo indicado por el rajá:
A la primera hija le corresponderían 1 perla y 1/7 de 35. Total 6 perlas y quedarían 30 a repartir.
La segunda, de las 30 perlas que quedaron, recibiría 2 y 1/7 de 28. Total 6 perlas y dejaría 24 a repartir.
La tercera recibiría 3 y 1/7 de 21. Total 6 y quedarían 18.
La cuarta 4 y 1/7 de 14. Total 6 y 12 a repartir.
La quinta 5 y 1/7 de 7. Total 6 y 6 a repartir.
Finalmente, la sexta hija recibiría las 6 perlas restantes.

Por tanto, la división propuesta por el rajá es justa y perfecta tal y como dictamina el juez.

Las hijas del rajá, las perlas y un reparto equitativo

“El hombre que calculaba” es un entretenido libro de Julio César de Mello Souza, más conocido por su seudónimo de Malba Tahan, que al tiempo que enseña Matemáticas las acompaña con historias orientales. A continuación se plantea un problema cuyo protagonista es Beremiz Shamir, el célebre calculista. Dice así:

Beremiz, por la mañana, recibió inesperadamente la visita honrosa del príncipe Cluzir Schá. La sala de la posada era pequeña para dar cabida a los ilustres visitantes. Beremiz, maravillado de la honrosa visita, descendió al patio a recibirlos.
El príncipe Cluzir, al llegar, saludó al calculista con un amistoso ‘zalam’, y le dijo:
‘El peor sabio es aquel que frecuenta a los ricos; el mayor rico es aquel que frecuenta a los sabios’.
‘Bien sé, señor – respondió Beremiz- que vuestras palabras son inspiradas por el más grande sentimiento de bondad. La pequeña e insignificante parte de ciencia que conseguí adquirir, desaparece ante la generosidad infinita de vuestro corazón’.
-‘Mi visita, calculista –interrumpió el príncipe- se debe más al egoísmo que al interés en la ciencia. Después que tuve el placer de oírlo, en casa del poeta Iezid, pensé en ofrecerle algún cargo de importancia en mi Corte. Deseo nombrarlo mi secretario o director del Observatorio de Delhi. ¿Acepta? Partiremos dentro de pocas semanas para la Meca y de allá para la India’.
-‘Desgraciadamente, ¡oh príncipe generoso! –respondió Beremiz-, no puedo ausentarme ahora de Bagdad. Sólo podré irme de aquí después que la hija del ilustre Iezid haya aprendido Matemática’.
Sonrió el maharajá y respondió:
‘Se el motivo de su negativa frente a ese compromiso, y creo que pronto llegaremos a un acuerdo. El sheik Iezid me ha dicho que la joven Telassim, dado los progresos que ha hecho, dentro de pocos meses estará en condiciones de enseñar a los ‘ulemas’ el famoso ‘problema de las perlas del Rajá’.
‘Yo mucho desearía –prosiguió el príncipe- conocer el complicado problema que viene desafiando la sagacidad de los algebristas y que se refiere, sin duda, a uno de mis gloriosos antepasados’.
Beremiz respondió:
‘Trátase más de una curiosidad aritmética que de un problema, y este es su enunciado’:

“Un rajá dejó a sus hijas cierto número de perlas y ordenó que el reparto se hiciese del siguiente modo: a la hija mayor correspondería una perla más un séptimo de las que quedasen; la segunda tomaría dos perlas y un séptimo de las restantes; la tercera recibiría tres perlas y un séptimo de las que quedasen. Y así sucesivamente, para las restantes hijas.

Las hijas más jóvenes presentaron su queja a un juez, alegando que por ese sistema complicado ellas serían fatalmente perjudicadas.
El juez –dice la tradición-, que era hábil en la resolución de problemas, respondió rápidamente que las demandantes estaban equivocadas, y que la división propuesta por el Rajá era justa y perfecta.

El juez tenía razón. Hecha la división, cada una de las hermanas recibió el mismo número de perlas.

Se pregunta: ¿Cuál es el número de perlas? ¿Cuántas las hijas del Rajá?”

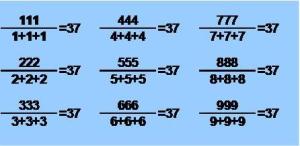
Ver solución en «Divisibilidad del número 37, truco o realidad matemática».

=====================================================================

A continuación mostramos la solución al problema planteado en el post: «Rectángulos, áreas y geometría».

Siguiendo la línea la reflejada por el matemático Ed Southall en su libro ‘Geometry Snacks’: “… Se trata de un libro en el que se dan al menos dos enfoques para la misma respuesta. El propósito es resaltar que hay múltiples vías disponibles y que son todas válidas y de igual valor…», se indican dos métodos diferentes para su resolución.

Método 1.-
Llamando S1 al área del cuadrado azul y S2 a la del cuadrado verde de la figura y dividiendo parcialmente sus áreas tal y como se señala, resulta:
S1= a+b+c
S2= b+d+e

Por otra parte:
a=e+x
d=c+x

Es decir:
S1=(e+x)+b+c= b+c+e+x
S2=b+(c+x)+e= b+c+e+x

Por tanto ambas áreas son iguales

Método 2.-
En la figura se puede ver que el área del triángulo rojo (M) inscrito tanto en el cuadrado azul como en el verde resulta ser:
M= ½ c*d= mitad del área cuadrado verde (c*d)
M= ½ a*b= mitad del área del cuadrado azul (a*b)

Por tanto, el área del triángulo rojo (M) es igual a la mitad del área de cada cuadrado. Es decir, las áreas de los cuadrados azul y verde son iguales.

Rectángulos, áreas y geometría

En un post anterior se planteó un problema del matemático Ed Southall, profesor de la Universidad de Huddersfield (Inglaterra), para el que no se requerían muchos conocimientos de geometría. Fue todo un reto que se hizo viral en la red social Twitter, en consonancia con la filosofía de su libro ‘Geometry Snacks’ que resume como:

“Se trata de un libro en el que se dan al menos dos enfoques para la misma respuesta. El propósito es resaltar que hay múltiples vías disponibles y que son todas válidas y de igual valor. Cuando enseñamos Matemáticas muchas veces promovemos nuestra solución sin explorar ninguna otra. Para mí hay una gran riqueza en la exploración de los diferentes enfoques. Hace que todos los métodos se sientan válidos, por lo que si un alumno lo ha hecho de otra manera, aún puede sentir la tranquilidad de haberlo hecho bien, mientras que lo que sucede a menudo es que si obtuvieron la respuesta correcta de una manera diferente a la de su maestro, sienten que su método es inferior».

En esa línea, Mikael Sundqvist propone el siguiente problema para el que no se proporciona ningún dato (ni medidas, ni ángulos) porque… no son necesarios. Dice así:

¿Cuál de los dos rectángulos de la figura tiene mayor área?

Ver solución en «Las hijas del rajá, las perlas y un reparto equitativo».

===========================================================================

A continuación mostramos la solución al problema planteado en el post: «Un problema de triángulos y la capacidad visual».

La respuesta es 18 triángulos.

Si se observa la figura existen 3 grupos de triángulos (Grupos 1, 2 y 3), cada uno formado por 6 triángulos distintos lo que hace un total de 18.

Un problema de triángulos y la capacidad visual

Se trata de un problema para el que no se necesitan conocimientos matemáticos, tan solo recordar la figura de un triángulo. En esta ocasión no valen por tanto excusas del tipo… ‘es que las matemáticas no es lo mío’, ‘yo es que soy de letras’ u otras en una línea similar. El enunciado, muy simple, dice así:

¿Cuántos triángulos hay en la figura adjunta?

Ver solución en «Rectángulos, áreas y geometría».

===========================================================================

A continuación mostramos la solución al problema planteado en el post: «El euro que falta y la suma de restos».

En este tipo de problemas lo mejor es aplicar una lógica ‘distinta’ a la que suele plantear el enunciado, normalmente con intención de confundir.

La realidad es que no falta ningún euro.

Se puede razonar, entre otras, de las dos siguientes maneras:

a) Mediante fracciones.
Cada uno de los tres amigos tendría que pagar 25/3 euros. Si además deciden dejar 2 euros de propina (2/3 de euro cada uno), cada amigo habría pagado 27/3 (9 euros). Lo que suma un total de 27 euros, que añadidos a 1 euro que cada uno se queda de la vuelta que les da el camarero hacen un total de 30 euros. Justo la cantidad que entregan para pagar la cuenta (3 billetes de 10 euros).

b) Viéndolo en su conjunto.
Si a la cuenta que asciende a 25 euros, le añadimos 3 euros que cogen de vuelta (1 cada uno de los tres amigos), más 2 euros que dejan de propina, el total es de 30 euros (3 billetes de 10 euros).

El euro que falta y la suma de restos

Hay muchas formas de calcular, pero no todas acertadas. Viene a cuento porque a veces un problema en apariencia sencillo nos lleva a la confusión precisamente por eso. Sobre todo cuando se hace con la operación o planteamiento hecho de una manera gráfica o escrita en un papel. ¡Suele entrar por los ojos! Además de manera fácil, sin lugar a la reflexión, ni siquiera alguna duda. Es el caso del problema que se expone a continuación. Dice así:

“Tres amigos están en una cafetería. Al pedir la cuenta, deciden pagar el importe a medias. El camarero les dice que asciende a 25 euros. Cada uno saca un billete de 10 euros, lo que hace un total de 30 euros. Les devuelven 5 monedas de 1 euro. Cada uno coge 1 moneda y generosos deciden dejar los 2 euros restantes de propina. Por tanto, cada uno ha pagado 9 euros (10 euros menos 1 que les devuelven), que multiplicados por tres (amigos) hacen un total de 27. Si a eso le añadimos los 2 euros de propina, hacen un total de 29.
La pregunta es: ¿Dónde está el euro que falta?”

Ver solución en «Un problema de triángulos y la capacidad visual».

============================================================================

A continuación mostramos la solución al problema planteado en el post: «Manzanas, naranjas y la lógica de las etiquetas».

Como el contenido de las tres cajas se encuentra mal etiquetado, se debe coger una fruta de la que dice ‘manzanas y naranjas’. Con esto será suficiente, pues solo se pueden dar las dos siguientes opciones:

– Al estar mal etiquetada, si es una manzana, solo podría ser la caja de manzanas. Por tanto, las naranjas estarían en la caja que pone ‘manzanas’, y la caja restante sería la de manzanas y naranjas.
– Si la fruta fuese una naranja, ésta sería la caja de naranjas, las manzanas estarían en la caja de ‘naranjas’ y en la caja que queda estarían las manzanas y naranjas.

Manzanas, naranjas y la lógica de las etiquetas

En esta ocasión se trata de un problema de lógica. Un tipo de problemas que siempre resulta atractivo porque consiste en buscar alternativas hasta dar con la solución. A veces interviene el pensamiento lateral, pero otras con el sentido común es suficiente. Dice así:

«Una frutería a la que acaban de llegar tres cajas de un reparto. Una contiene sólo manzanas; otra, sólo naranjas; y la tercera, manzanas y naranjas. Cada caja tiene una etiqueta distinta (‘manzanas’, ‘naranjas’ y ‘manzanas y naranjas’), pero ninguna tiene la etiqueta que le corresponde.

¿Cómo se puede saber la fruta que contiene cada una de las cajas sacando una sola pieza de una sola de ellas?»

Ver solución en «El euro que falta y la suma de restos».

===========================================================================

A continuación mostramos la solución al problema planteado en el post: «Un problema de triángulos, áreas y semejanzas, una manera de recordar conceptos».

En la figura se puede observar que los triángulos 1 y 2 son semejantes porque tienen todos sus ángulos iguales. Además, la base del triángulo 2 es igual al lado del cuadrado y la del triángulo 1 a la mitad del mismo. Por otra parte, una propiedad de los triángulos semejantes es que la razón entre sus alturas es igual a la existente entre dos lados homólogos.

Si llamamos h1 y h2 a las alturas y c al lado del cuadrado se pueden establecer las siguientes relaciones:

Por tanto el área del triángulo 2 es igual a 1/3 del área del cuadrado.

Un problema de triángulos, áreas y semejanzas y una manera de recordar conceptos

Se trata de un reto que el matemático Ed Southall, profesor de la Universidad de Huddersfield (Inglaterra), lanzó a través de la red Twitter provocando un auténtico boom. Pronto se hizo viral. Muchos lo compartieron, bastantes admitieron haber estado horas intentando resolverlo y casi todos sin dar con la solución correcta. Un problema que aplicando conocimientos no demasiado complicados de geometría, tantas veces olvidados, lo hubiesen hecho más sencillo. Dice así:

“En la imagen de la figura se puede ver un triángulo ‘rosa’ dentro de un cuadrado. La pregunta es: ‘¿Qué fracción del cuadrado se encuentra sombreada en color ‘rosa’?”

Ver solución en «Manzanas, naranjas y la lógica de las etiquetas».

Ed Southall señala que lo que más le sorprendió de las respuestas dadas en Twitter fueron  los muchos razonamientos que había detrás de las soluciones, algo que encajaba muy bien con la filosofía de su último libro, ‘Geometry Snacks’, donde presenta 53 rompecabezas y las distintas formas de resolverlos. Lo resume en: “Se trata de un libro en el que se dan al menos dos enfoques para la misma respuesta. El propósito es resaltar que hay múltiples vías disponibles y que son todas válidas y de igual valor. Cuando enseñamos Matemáticas muchas veces promovemos nuestra solución sin explorar ninguna otra. Para mí hay una gran riqueza en la exploración de los diferentes enfoques. Hace que todos los métodos se sientan válidos, por lo que si un alumno lo ha hecho de otra manera, aún puede sentir la tranquilidad de haberlo hecho bien, mientras que lo que sucede a menudo es que si obtuvieron la respuesta correcta de una manera diferente a la de su maestro, sienten que su método es inferior».

Antes de ser profesor universitario en Huddersfield, Ed Southall era Jefe de Matemáticas en una escuela secundaria de Sheffield. Es entonces cuando comienza a replantearse el enfoque de la asignatura, haciendo hincapié en ‘comprender’ las Matemáticas en lugar de aprenderlas de memoria: “Es ahí cuando obtienes la iluminación de qué se trata la Matemática y por qué es hermosa». En el año 2012 empieza por presentar un acertijo matemático cada semana para ser resuelto por los docentes de su departamento: «Lo hice para generar más entusiasmo sobre las Matemáticas y para revitalizar su amor por el tema. Luego comencé con la Web y como la respuesta fue muy buena… seguí». Algo que más tarde extendió a Twitter, red social donde cuenta con miles de seguidores.

===========================================================================

A continuación mostramos la solución al problema planteado en el post: «El automóvil y los círculos concéntricos».

En la figura se puede observar que en el giro concéntrico del automóvil se describen dos perímetros, dos círculos, uno de radio r y otro de radio r+2, cuya longitud sería:

P (interior)= 2πr y
P (exterior)= 2π (r+2)

Por otra parte se indica que las ruedas exteriores dan el doble número de vueltas que las interiores. Es decir, el perímetro exterior tendría una longitud doble que el interior. O lo que es lo mismo:

4πr= 2π (r+2) = 2πr + 4.
Por tanto r=2

Y el perímetro exterior:
P (exterior)= 8 π

El automóvil y los círculos concéntricos

Se trata de un sencillo ejercicio de geometría elemental. Hasta niños de primaria son capaces de resolverlo. Solo requiere recordar las propiedades de la circunferencia y el círculo. Dice así:

“Para probar la capacidad de giro de un automóvil se le hace describir un círculo de tal modo que las ruedas exteriores dan doble número de vueltas que las interiores. La separación entre las ruedas de un mismo eje es de 2 metros. ¿Cuál es el perímetro del círculo exterior?”

Ver solución en «Un problema de triángulos, áreas y semejanzas y una manera de recordar conceptos».

=============================================================================================

A continuación mostramos la solución al problema planteado en el post: «Una atrayente ecuación numérica, un problema para una mente lógica».

En su enunciado ya dábamos una pista por donde debería actuar la lógica. Se señalaba:
“Como complemento, decir que el resultado de cada una de las igualdades planteadas se forma de la siguiente manera: primero se deben restar los dos números y luego sumarlos. Así por ejemplo: 6 – 4 = 2 y 6 + 4 = 10; entonces, 2 y 10 da como resultado 210. Igual con el resto de los citados”.

Por tanto, los números buscados serían: 12 y 11
Y la ecuación o secuencia 12+11=123 (12-11=1 y 12+11=23).
O lo que es lo mismo, primero se deben restar los números para la primera cifra y luego sumarlos para la segunda.

Una atrayente ecuación numérica, un problema para una mente lógica

En el post del último problema planteado salió a relucir por primera vez el nombre de Presh Talwalkar, matemático estadounidense autor de ‘The Joy of Game Theory’, una introducción al pensamiento estratégico, quien además de su faceta profesional tiene un blog personal y un canal en YouTube donde publica interesantes problemas matemáticos. A continuación reflejamos uno de los ejercicios que puso a prueba a muchos usuarios de la red social Facebook, al sentirse atraídos según el periódico ‘Daily Mail’ por la ‘propuesta’ de querer demostrar que poseían un coeficiente intelectual mayor de 150. Dice así:

“En el cuadro de la figura se plantea la siguiente relación o ecuación numérica: 6 + 4 = 210; 9 + 2 = 711; 8 + 5 = 313; 5 + 2 = 37; 7 + 6 = 113; 9 + 8 = 117; 10 + 6 = 416 y 15 + 3 = 1218.
La pregunta es: ¿Cuales serían los dos números que darían como resultado 123?

Como complemento de información, decir que el resultado de cada una de las igualdades planteadas se forma de la siguiente manera: primero se deben restar los dos números y luego sumarlos. Así por ejemplo: 6 – 4 = 2 y 6 + 4 = 10; entonces, 2 y 10 darían como resultado 210. Igual con el resto de números y ecuaciones citadas».

Ver solución en «El automóvil y los círculos concéntricos».

===========================================================================

A continuación mostramos la solución al problema planteado en el post: «Como calcular la altura de una mesa por niños de educación primaria».

Lo primero recordar que se trata de un ejercicio propuesto a alumnos de primaria cuyos conocimientos matemáticos son escasos. Por tanto lo lógico sería encontrar la solución sin recurrir, por ejemplo, a ecuaciones, probablemente el método utilizado por la mayoría de los adultos.

Como se puede observar, en principio para calcular la altura de la mesa solo se cuenta con las dos medidas indicadas en las figuras de su enunciado. En la primera aparecen un gato encima de la mesa y una tortuga en el suelo indicando que la altura desde lo alto del caparazón de la tortuga hasta la cabeza del gato es de 170 cm.; mientras que en la segunda, con los dos animales intercambiados de sitio, se señala que la altura desde la cabeza del gato al caparazón de la tortuga es de 130 cm.

La solución consistiría en colocar una mesa encima de la otra. De esa manera se puede observar como de forma solo visual su altura es de 150 cm. (2 mesas=300 cm.).

Para aquellos que no dieron con esta solución, recurriendo finalmente a las ecuaciones el planteamiento sería el siguiente:
gato + mesa – tortuga = 170
tortuga + mesa – gato = 130

Si sumamos ambas ecuaciones, se eliminarían los términos de gato y tortuga (se anulan entre sí), llegando a la misma solución que con el método visual utilizado por los niños de primaria. Es decir:
2 mesas= 170 + 130 = 300
Y por tanto la altura de la mesa sería de 150 cm.