Un número es una cantidad o magnitud que representa una propiedad o función concreta de un objeto. Se trata de un concepto que se suele asociar a la capacidad para contar y también a la de comparar cuando dos conjuntos similares uno es mayor que otro. Las primeras sociedades humanas ya se encontraron con esta última tesitura, así como conocer con exactitud de cuantos elementos estaba formado cada conjunto. Sin embargo, la habilidad o capacidad de saber contar del ser humano no es un fenómeno tan simple. No todos los pueblos o culturas tenían métodos de conteo lo suficientemente amplios. Se cree que los primeros sistemas se iniciaron mediante el uso de objetos físicos (p.e. montones de piedras) o marcas (p.e. en huesos tallados). Referente a los sistemas numerales parece que la operación de contar estaba relacionada, aunque no siempre, al conteo con los dedos. De ahí que el sistema de base decimal fuese el más utilizado. Ahora bien, a medida que la ciencia avanzaba otros números, no menos importantes, fueron tomando acto de presencia, sobre todo en el mundo científico. Se suele afirmar que desde hace 5000 años la mayoría de las civilizaciones contaban tal y como lo hacemos en la actualidad; si bien, aunque todas representaban con exactitud los números naturales, su forma de escribirlos no siempre era la misma. Sin embargo, sobre lo que no existen dudas es que… los números, las cifras, nos han acompañado siempre.
Con este post iniciamos las curiosas historias que, por su significado u origen, rodean a algunos números muy conocidos o a menudo utilizados. Incluiremos también diversas anécdotas sobre nuestra predilección por determinados números en concreto. Comenzaremos con el número cero (0) y el número pi (π).
Número ‘cero’ (0)
Antes de hacer un breve recorrido por su historia, como complemento de información conviene recordar que un sistema de numeración es un conjunto de símbolos que sirve para asignar un determinado valor a los números. Se clasifican en dos grandes grupos: sistemas posicionales y no posicionales. En los posicionales el valor de un dígito depende tanto del símbolo utilizado como de la posición que ocupa en el número, mientras que en los no posicionales los dígitos tienen el valor del símbolo, no dependiendo de la posición o columna en que se encuentren. La cantidad de símbolos permitidos en un sistema de numeración posicional se conoce como base del sistema. Así, si decimos que un sistema tiene base X quiere decir que existen X símbolos diferentes para escribir los números y que X unidades componen una unidad de orden superior. Por ejemplo, en el sistema de numeración decimal, el más utilizado, si contamos desde 0 e incrementamos una unidad cada vez, al llegar a 9 unidades ya no existen más símbolos disponibles. Es decir, para seguir contando lo que hacemos es añadir una nueva columna a la izquierda del número, volviendo a utilizar de nuevo sus símbolos (en este caso 10, del 0 al 9) formando entonces una unidad de primer orden (decena). Y así sucesivamente a medida que se va ampliando.
El cero (0) es el signo o símbolo numérico de valor nulo. Su historia como tal valor no es muy antigua. Si bien grandes y antiguas civilizaciones (Egipto, Babilonia, Grecia o Maya) disponen de documentos matemáticos o astronómicos mostrando símbolos indicativos del valor cero, no lo pudieron aplicar o introducir como tal por las distintas peculiaridades de sus sistemas numéricos. Se cree que el cero apareció por primera vez en Babilonia en el siglo III a.C., aunque su escritura parece que se remonta al año 2000 a.C. Los babilonios, que escribían en arcilla sin cocer sobre superficies planas o tablillas, utilizaban un sistema de base 60 en el que no era posible distinguir por ejemplo el número 15 del 105 o del 1005. Es alrededor del año 400 a.C. cuando comienzan a colocar el signo de ‘dos cuñas’ en los lugares ocupados por el cero. También se tiene constancia antes de la era cristiana del uso del cero en Mesoamérica, correspondiendo a la cultura maya en el año 36 a.C. el primer documento con este símbolo en su sistema de numeración. Los romanos no lo utilizaban ya que sus números se representaban por agrupación o suma de letras del alfabeto: I, V, X, L, C, D, M (así por ejemplo: MCLI=1151).
Aunque todavía no está claro quien fue su inventor, se cree que fue en la India, hacia el año 650, cuando ‘nació’ el cero (0) como valor nulo. Cuna de la numeración posicional, se apunta a que fue el matemático Brahmagupta el primero en teorizar sobre el concepto de ‘cero’. Lo que ofrece menos dudas es que el sistema de numeración decimal (0 al 9) pasó desde la India a la cultura árabe y de allí a Europa. Si bien se atribuyen los primeros usos del cero a Francia o al controvertido papa Silvestre II, alrededor del año 1000, la mayor parte de las referencias indican que fue introducido en Europa en el año 1202 por el matemático italiano Leonardo de Pisa, también conocido por Fibonacci, que lo describe en una de sus obras, ‘Liber abaci`’ (‘Libro del ábaco’), mostrando el álgebra árabe y elogiando las grandes ventajas respecto al sistema de numeración romano.
El cero, símbolo de valor nulo (0), forma parte del sistema de numeración decimal, el más utilizado en todo el mundo, donde según el lugar en que se encuentre hace que otros números cambien de valor.
Número ‘pi’ (π)
El número π (pi), uno de los números más famosos de la historia, representa la relación entre la longitud de una circunferencia y su diámetro. Se trata de un número irracional, que a diferencia de los números racionales no se pueden representar por el cociente exacto de dos números enteros (fracción), ya que su expresión decimal ni es exacta ni periódica. Su valor real, truncado en sus primeras cifras, es 3,14159265358979323846… y así hasta el infinito. Se puede observar que la secuencia de sus cifras no se repite.
Al número π se le recuerda muchas veces como 3,1416 (tres, catorce, dieciséis), pero sobre todo como 3,14 (tres, catorce). De ahí que el 14 de marzo (3- mes, 14- día) haya sido declarado o se le conozca como el día del número pi. Su nombre o símbolo π, letra griega pi, procede de la inicial (la misma) de dos palabras griegas (‘periferia’ y ‘perímetro de un círculo’). Fue propuesto en 1706 por el matemático inglés William Jones, aunque fue el suizo Leonhard Euler, seguramente el matemático más importante del siglo XVIII y uno de los más grandes de todos los tiempos, quien en 1748 lo difundió y popularizó de forma definitiva en su famosa obra dedicada al cálculo infinitesimal. La búsqueda de su valor con el mayor número de decimales ha sido constante a lo largo de la historia. De una forma resumida a continuación se señalan alguno de sus hitos más importantes.
En las culturas antiguas como el Antiguo Egipto se remonta al año 1800 a.C. Está descrito en un papiro (Rhind) donde se señala un valor aproximado de π indicando que el área de un círculo es similar a la de un cuadrado cuyo lado es igual al diámetro del círculo disminuido en 1/9 (es decir, 8/9 del diámetro). O lo que es lo mismo π=256/81 (4*64/81)= 3,1649…
En Grecia, el matemático Arquímedes (siglo III a. C.) fue capaz de determinar el valor de π entre el intervalo comprendido por 3 10/71 (223/71), como valor mínimo, y 3 1/7 (22/7), como valor máximo, lo que significa una aproximación con un error entre 0,024 % y 0,040 % sobre su valor real. Su método era muy simple y al ser los griegos desconocedores de los números decimales lo expresó como fracción. Consistía en circunscribir e inscribir polígonos regulares de n lados en circunferencias y calcular su perímetro. Comenzó con hexágonos, pero fue doblando el número de lados hasta llegar a polígonos de 96 lados. Alrededor del año 20 d. C., en Italia, el ingeniero romano Vitruvio calculó el número π como el valor fraccionario 25/8 midiendo la distancia recorrida en una revolución por una rueda de diámetro conocido. Hacia el año 150 d. C., el astrónomo y geógrafo griego Ptolomeo equiparó a π a 3,1416. En 1600, el profesor de matemáticas alemán Ludolph van Ceulen (a lo largo de su vida) fue capaz de calcular el valor de π llegando a utilizar polígonos de millones de lados, un trabajo que fue muy reconocido, tanto que como homenaje póstumo se grabaron sobre su tumba las 36 cifras a las que llegó. A finales del siglo XIX, el matemático inglés William Shanks calculó a mano 707 decimales (tardó veinte años), aunque luego se descubrió que había un error en el proceso y solo eran correctas las 527 primeras cifras. Y ya en el siglo XX, con la ayuda de la informática (computadores), se avanzó a pasos agigantados hasta llegar a miles de millones de dígitos, cifra que se ha superado ampliamente en el año 2009 llegando con la ayuda de una supercomputadora a más de dos billones y medio de decimales, reto que ha quedado para cuando se desarrollen nuevas técnicas.
Tan solo añadir a título de curiosidad acerca del número π, al que casi siempre se recuerda de nuestra educación matemática básica, aunque se trata de un número irracional y por tanto no tiene ninguna secuencia que se repita en su expresión decimal, entre las posiciones 762 y 767 se produce un hecho caso curioso: aparecen seis nueves seguidos. Una ubicación conocida con el nombre de punto de Feynman debido a un comentario simpático de Richard Phillips Feynman, famoso físico estadounidense, quien decía: «Me gustaría memorizar todos los decimales de π hasta esa posición para terminar diciendo: «…9, 9, 9, 9, 9, 9 y así sucesivamente’’, Afirmaba en tono de broma que de esa manera sería un número racional, algo que solo podría ser posible si a partir de ese punto todas las cifras fueran nueves.
Solo decir como final que, si bien los diez dedos de las manos fueron la base inicial del sistema decimal, los números siempre han acompañado a la humanidad. El número 0 y el número π son un buen ejemplo.
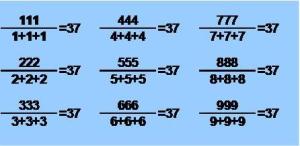
“Tal y como muestra la imagen, se plantea el siguiente ejercicio:
Supongamos un número genérico de tres cifras: AAA.
Escrito por eltrasterodepalacio 
El trastero de Palacio 